本笔记根据屈婉玲教授编写的《离散数学及其应用整理》
持续更新中
第一章:命题逻辑的基本概念
1.1 命题与连结词
命题的相关定义:
- 命题:能判断其真值的陈述句
- 真值:真、假(0,1)
- 真命题:真值为真的命题
- 假命题:真值为假的命题
- 简单命题(原子命题):不能被分解为更简单的命题的命题
- 复合命题:由原子命题通过连结词组合成的命题
关于命题的判断:
- 判断是否为陈述句
- 判断它是否有唯一真值
关于连结词:
- 否定连结词(非)
- 合取连结词(交)
- 析取连结词(并)
- 蕴含连结词(非p并q)
- 等价连结词(相等)
注意:连结词运算顺序
(),┐,∧,∨,→
1.2 命题公式及其赋值
命题公式相关定义:
- 命题常项(命题常元):真值确定,不可改变的命题
- 命题变项(命题变元):真值可以变化的命题
- 合式公式(命题公式):将命题变项用连结词和圆括号按一定逻辑关系连接起来的符号串
- 子公式:合式公式中也为合式公式的一部分
- 重言式(永真式):在所有赋值下取值均为真的命题公式
- 矛盾式(永假式):在所有赋值下取值均为假的命题公式
- 可满足式:不是矛盾式的命题公式
赋值相关定义:
- 赋值:给公式A的全部命题变项指定一个真值
- 成真赋值:使公式A为1的一组值
- 成假赋值:使公式A为0的一组值
- 真值表:公式A在所有情况下的取值情况列成的表
第二章:命题逻辑等值演算
2.1 等值式
设A,B是两个命题公式,若A,B构成的等价式A↔B为重言式,则称A与B是等值的

注意:用等值演算不能直接证明两个公式不等值
2.2 析取范式与合取范式
- 文字:命题变项及其否定
- 简单析取式:仅由有限个文字构成的析取式
- 简单合取式:仅由有限个文字构成的合取式
- 析取范式:由有限个简单合取式的析取构成的命题公式
- 合取范式:由有限个简单析取式的合取构成的命题公式
主析取范式与主合取范式:
极小项的概念:
- 简单合取式
- 每个命题变项和它的否定式恰好出现且仅出现一次
- 命题变项或它的否定式按照下标从小到大排列
极大项的概念:
- 简单析取式
- 每个命题变项和它的否定式恰好出现且仅出现一次
- 命题变项或它的否定式按照下标从小到大排列
注意:
- n个命题变项有2n个极小项和2n个极大项
- 2n个极小项(极大项)均互不等值
- 用mi表示第i个极小项,其中i是该极小值成真赋值的十进制表示。用Mi表示第i个极大项,其中i是该极大项成假赋值的十进制表示
主析取范式:
所有简单合取式都是极小项的析取范式
主合取范式:
所有简单析取式都是极大项的合取范式
连结词的完备集:
设S是一个连结词集合,如果任一命题公式可以由仅含S中的连接词构成的公式表示,则称S是一个连结词完备集。
第三章:命题逻辑的推理理论
3.1 推理的相关公式
推理:单向箭头,左边是前提,右边是结论
- 设A和B是两个命题公式,当且仅当A→B是重言式时,称从A可推出B或B是前提A的有效结论,记为A⇒B
- 命题公式A1,A2,……,Ak推出B的推理正确当且仅当A1^A2^……^Ak→B为重言式
- 推理的前提:A1,A2,……,Ak
- 推理的结论:B
推理公式:

3.2 自然推理系统
例1:

例2:

例3:
附加前提法

例4:这里使用了归谬法,可以多引入一个否定的结论

第四章:一阶逻辑的基本概念
4.1 谓词逻辑命题符号化
谓词逻辑命题符号化的三个基本要素:个体词、谓词和量词
1.个体词:
- 个体词:研究对象中可以独立存在的具体的或抽象的个体(如:小智 中国 3)
- 个体常项:表示具体或特定的客体的个体词
- 个体变项:表示抽象或泛指的个体词
- 个体域(论域):个体变项的取值范围(可以理解为定义域)
- 全总个体域:由宇宙间一切事物组成的个体域
2.谓词:
- 谓词:刻画个体词性质及个体词之间相互关系的词
- 谓词常项:表示具体性质或关系的谓词
- 谓词变项:表示抽象或泛指的性质或关系的谓词
- n元谓词:含n个个体变项的谓词P
- 0元谓词:不带个体变项的谓词(当某0元谓词为谓词常项时,该0元谓词为命题)
3.量词:
- 量词:个体之间数量关系的词
- 全称量词:表示个体域中所有的x
- 存在量词:表示个体域中有一个个体x
4.2 谓词逻辑公式及其解释
在公式∀xA和∃xA中,称x为指导变元,A为量词的辖域。在∀x和∃x的辖域中,x的所有出现的称作约束出现,A中不是约束出现的其他变项均称作自由出现。
例如:
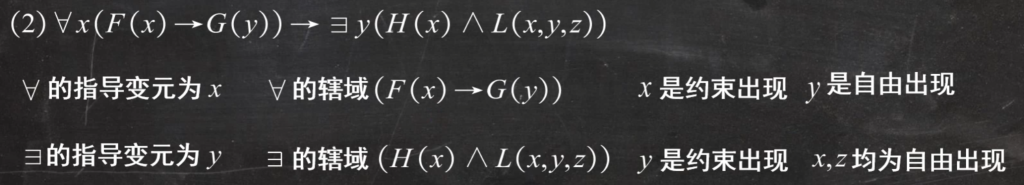





Comments NOTHING