Warshall算法求传递闭包矩阵
1.什么是传递闭包?
在深入了解Warshall算法之前,我们先要明白目标是什么。
传递闭包:对于一个有向图 G,它的传递闭包是另一个图 G,G 和 G 拥有相同的顶点。如果在原图 G 中,从顶点 i 到顶点 j 存在一条路径(路径长度可以大于1),那么在 G* 中就存在一条从 i 直接指向 j 的边。
简单来说,传递闭包就是回答这样一个问题:“从任意一个点出发,我能到达哪些其他的点?” 如果能到达,就连一条直接的边。
举个例子: 如果 A → B,且 B → C,那么在传递闭包中,除了原有的 A→B 和 B→C,我们还会新增一条 A→C 的边。
Warshall算法就是用来高效计算这个传递闭包的利器。
2.Warshall算法的核心思想
Warshall算法的精髓在于“逐步引入中间点”。
想象一下,我们想知道从城市 i 能否到城市 j。一开始,我们只看有没有直达的航班。后来,我们允许在城市1中转,看看会不会增加新的可达路线。接着,我们再允许在城市2中转,看看会不会又增加新的路线……直到我们把所有城市都当作过中转站考虑了一遍,最终得到的就是完整的可达性网络。
算法就是这样工作的:
外层循环 (k):遍历所有顶点,每次把一个顶点 k 当作“允许的中间点”。 内层循环 (i, j):遍历所有顶点对 (i, j),检查“如果允许经过 k,i 能否到达 j?” 核心判断逻辑: 对于任意顶点 i, j, k: 如果 i 能到达 k 并且 k 能到达 j,那么 i 就能到达 j。
这个逻辑用邻接矩阵来表示就是: R[i][j] = R[i][j]OR(R[i][k]ANDR[k][j])
这里的 R 就是我们的可达性矩阵,算法开始时它是图的邻接矩阵,结束时它就是传递闭包矩阵。
3.实例演示
上面的定义可能比较晦涩难懂,那么我们不妨举个例子实际操作一下。
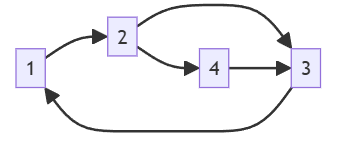
这个图有4个顶点:{1, 2, 3, 4}。
步骤1:建立初始邻接矩阵 R⁰
我们用一个4x4的矩阵 R 来表示这个图。R[i][j] = 1 表示存在从 i 到 j 的直接边,0 表示没有。
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 1 |
| 3 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 |
这个矩阵就是我们算法的起点,我们称之为 R⁰。
步骤2:开始迭代运算
我们将进行4次迭代,分别对应 k=1, 2, 3, 4。每次迭代都会生成一个新的矩阵 R¹, R², R³, R⁴。
迭代1:允许顶点 1 作为中间点 (k=1)
我们的目标是:检查所有顶点对 (i, j),看是否能通过顶点1建立新的连接。即,判断 R[i][1] 和 R[1][j] 是否都为1。
- R⁰[3][1] = 1(3 → 1)
- R⁰[1][2] = 1(1 → 2)
根据逻辑 R[3][2] = R[3][2]OR(R[3][1]ANDR[1][2]),我们发现: R[3][2] = 0OR(1AND1) = 1。 这意味着,通过顶点1,我们发现了一条从 3 到 2 的新路径 (3 → 1 → 2)。
我们检查所有其他组合,没有发现新的连接。于是,我们更新矩阵,得到 R¹:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 1 |
| 3 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 |
迭代2:允许顶点 2 作为中间点 (k=2)
现在,我们基于 R¹ 进行计算,允许顶点2作为中间点。即判断 R¹[i][2] 和 R¹[2][j]。
- R¹[1][2] = 1 (1→2)
- R¹[3][2] = 1 (3→2)
- R¹[2][3] = 1 (2→3)
- R¹[2][4] = 1 (2→4)
我们检查所有 (i, j) 对:
- i=1, j=3: R¹[1][3] = R¹[1][3]OR(R¹[1][2]ANDR¹[2][3]) = > 0OR(1AND1) = 1。新增路径 1 → 2 → 3。
- i=1, j=4: R¹[1][4] = R¹[1][4]OR(R¹[1][2]ANDR¹[2][4]) = > 0OR(1AND1) = 1。新增路径 1 → 2 → 4。
- i=3, j=3: R¹[3][3] = R¹[3][3]OR(R¹[3][2]ANDR¹[2][3]) = > 0OR(1AND1) = 1。新增路径 3 → 2 → 3。
- i=3, j=4: R¹[3][4] = R¹[3][4]OR(R¹[3][2]ANDR¹[2][4]) = > 0OR(1AND1) = 1。新增路径 3 → 2 → 4。
更新矩阵,得到 R²:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 |
| 2 | 0 | 0 | 1 | 1 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 1 | 0 |
迭代3:允许顶点 3 作为中间点 (k=3)
现在,我们基于 R² 进行计算,允许顶点3作为中间点。即判断 R²[i][3] 和 R²[3][j]。
- R²[1][3] = 1(1 → 3)
- R²[2][3] = 1(2 → 3)
- R²[3][3] = 1(3 → 3)
- R²[4][3] = 1(4 → 3)
- R²[3][1] = 1(3 → 1)
- R²[3][2] = 1(3 → 2)
- R²[3][4] = 1(3 → 4)
我们检查所有 (i, j) 对:
- i=1, j=1: R²[1][1] = R²[1][1]OR(R²[1][3]ANDR²[3][1]) = > 0OR(1AND1) = 1。新增路径 1 → 3 → 1。
- i=1, j=2: R²[1][2] 已经是1,无需更新。
- i=2, j=1: R²[2][1] = R²[2][1]OR(R²[2][3]ANDR²[3][1]) = > 0OR(1AND1) = 1。新增路径 2 → 3 → 1。
- i=2, j=2: R²[2][2] = R²[2][2]OR(R²[2][3]ANDR²[3][2]) = > 0OR(1AND1) = 1。新增路径 2 → 3 → 2。
- i=4, j=1: R²[4][1] = R²[4][1]OR(R²[4][3]ANDR²[3][1]) = > 0OR(1AND1) = 1。新增路径 4 → 3 → 1。
- i=4, j=2: R²[4][2] = R²[4][2]OR(R²[4][3]ANDR²[3][2]) = > 0OR(1AND1) = 1。新增路径 4 → 3 → 2。
- i=4, j=4: R²[4][4] = R²[4][4]OR(R²[4][3]ANDR²[3][4]) = > 0OR(1AND1) = 1。新增路径 4 → 3 → 4。
更新矩阵,得到 R³:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 1 | 1 | 1 | 1 |
迭代4:允许顶点 4 作为中间点 (k=4)
最后,我们基于 R³ 进行计算,允许顶点4作为中间点。即判断 R³[i][4] 和 R³[4][j]。
观察 R³,我们发现 R³[1][4], R³[2][4], R³[3][4], R³[4][4] 都为1。 同时,R³[4][1], R³[4][2], R³[4][3] 也都为1。
这意味着通过顶点4,我们可以从1、2、3、4到达1、2、3、4。但是,当我们检查 R³[i][j] 时,发现这些位置都已经是1了。
例如: 检查 i=1, j=1:R³[1][1] 已经是1,无需更新。 检查 i=1, j=2:R³[1][2] 已经是1,无需更新。 …
经过检查,我们发现没有任何新的连接需要添加。所以 R⁴ = R³。
步骤三:得出最终结果
算法结束,最终的矩阵 R⁴ 就是原图的传递闭包矩阵。
传递闭包矩阵 R⁴:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 1 | 1 | 1 | 1 |
解读这个结果:
这个矩阵告诉我们,在这个图中,从任何一个顶点出发,都可以到达其他所有顶点(包括它自己)。例如,R⁴[4][1] = 1 意味着从顶点4到顶点1存在路径(4 → 3 → 1)。
我们可以画出这个传递闭包对应的图,它是一个包含所有可能边的完全图(包括自环)。
4.总结
Warshall算法通过三层嵌套循环,系统地、逐步地考虑将每个顶点作为路径的中间节点,不断更新可达性矩阵,直到所有可能的路径都被发现。虽然时间复杂度是 O(n³),但对于邻接矩阵表示的图来说,它的实现非常简洁高效,是求传递闭包问题的标准解决方案。
