Kruskal算法:

在离散数学中，Kruskal 算法是一种用于求解带权无向连通图的最小生成树（MST）的经典算法。

它的核心思想非常直观:贪心策略。也就是说，我们总是试图从图中挑选出当前权重最小的那条边，只要这条边不与已经挑选出的边形成回路（环），就把它加入到生成树中。

下面，我将通过一个示例直接演示Kruskal算法的操作方法。

1.算法核心步骤

在开始实例之前，先记住 Kruskal 算法的三个核心步骤：

排序：将图中所有的边按照权重从小到大进行排序。
选边：从权重最小的边开始考察。
判环：
- 如果这条边连接的两个顶点目前不在同一个连通分量里（即加入这条边不会形成回路），就选中这条边，加入生成树。
- 如果这条边加入后会形成回路，就丢弃这条边。
结束：重复步骤 2 和 3，直到选够了n − 1条边(n是顶点数)，或所有边都考察完了

2.实例设定

假设我们有一个带权无向图，包含 5 个顶点:A,B,C,D,E。

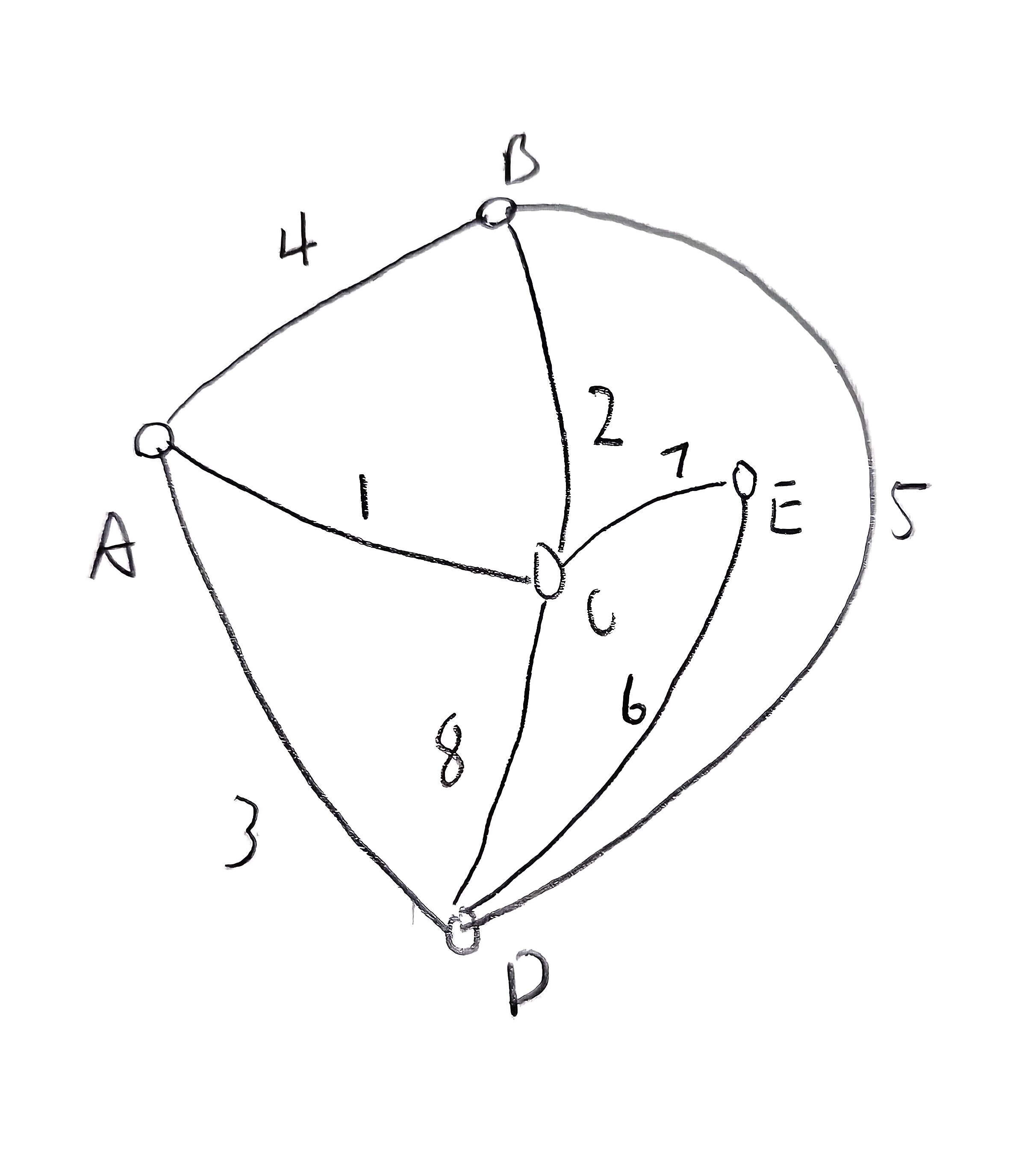
(A,B) : 权重 4
(A,C) : 权重 1
(A,D) : 权重 3
(B,C) : 权重 2
(B,D) : 权重 5
(C,D) : 权重 8
(C,E) : 权重 7
(D,E) : 权重 6

我们的目标是求出这棵图的最小生成树及其总权重。

3.详细运算步骤

第一步:对所有边按权重进行排序（升序）

这是 Kruskal 算法的第一步工作，我们需要列出一个有序的边表:

排序	边	权重
1	(A,C)	1
2	(B,C)	2
3	(A,D)	3
4	(A,B)	4
5	(B,D)	5
6	(D,E)	6
7	(C,E)	7
8	(C,D)	8

第二步:逐步选边并判环

我们要从上表依次选取边。为了方便判环，我们可以记录当前的连通分量情况（即哪些点已经连在一起了）。

初始状态

每个点都是独立的：{A},{B},{C},{D},{E} 已选边数:0 目标边数:5−1=4 条

1.考察边(A,C)，权重1

判断:A在集合{A}，C在集合{C}。两者不同，不连通。
决策：选中这条边。
更新状态:
- 已选边:{(A,C)}
- 连通分量合并:{A,C},{B},{D},{E}

2.考察边(B,C)，权重2

判断:B在集合{B}，C在集合 {A,C}。两者不同。
决策:选中这条边。
更新状态:
- 已选边:{(A,C),(B,C)}
- 连通分量合并:B连入了{A,C}，变成了{A,B,C}，剩余{D},{E}。

3.考察边(A,D)，权重3

判断:A在集合{A,B,C}，D在集合{D}。两者不同。
决策:选中这条边。
更新状态:
- 已选边:{(A,C),(B,C),(A,D)}
- 连通分量合并:D连入，变成了{A,B,C,D}，剩余{E}。

4.考察边(A,B)，权重4

判断:A在集合{A,B,C,D}，B也在集合{A,B,C,D}。
决策：丢弃这条边。因为A和B现在已经是连通的（通过 A−C−B），如果加上这条边，就会在A,B,C之间形成一个环路。
更新状态：无变化。

5.考察边(B,D)，权重5

判断:B在集合{A,B,C,D}，D也在集合{A,B,C,D}。
决策：丢弃这条边。
更新状态：无变化。

6.考察边(D,E)，权重6

判断:D在集合{A,B,C,D}，E在集合{E}。两者不同。
决策:选中这条边。
更新状态:
- 已选边:{(A,C),(B,C),(A,D),(D,E)}
- 连通分量合并:所有点合成{A,B,C,D,E}。

第三步：结束算法

此时:

我们已经选了 4 条边（A − C, B − C, A − D, D − E）。
顶点总数是 5 个，n − 1 = 4。
所有顶点都已经连通。算法结束！不需要再考察剩余的 (C, E) 和 (C, D)。

4. 最终结果

通过上述步骤，我们构建出的最小生成树包含以下边:

A → C (权重 1)
B → C (权重 2)
A → D (权重 3)
D → E (权重 6)

最小生成树的总权重 = 1 + 2 + 3 + 6 = 12

5. 图解总结

我们可以想象一下连线的顺序：

先把 A 和 C 连起来（最便宜）。
再把 B 连到 C 上。
再把 D 连到 A 上。现在 A, B, C, D 是一个大块。
看 A − B 和 B − D，发现它们都在这个大块内部，连了会有圈，所以不要。
最后把孤立的 E 连到 D 上（或者连到 A, B, C 上都行，但在本题列表中正好是 D − E 最先出现且合法）。

总结

Kruskal算法的难点主要在于如何判断是否形成回路。在做手工计算时，你可以像我上面那样，在草稿纸上维护几个集合（比如 {A, C}），每次看边连接的两个点是否在同一个集合里。

不在同一个集合：连线，合并集合。
在同一个集合：跳过，防止成环。

Prim算法:

在离散数学中，Prim 算法（普里姆算法）是另一种求带权无向连通图的最小生成树（MST）的经典算法。

与 Kruskal 算法（从边入手，全局找最小边）不同，Prim 算法的核心思想是从点入手，步步为营。它从一个起始顶点开始，每次寻找一个与当前生成的树“距离最近”（即连接边的权重最小）的邻接点，将其纳入树中，直到包含所有顶点。

下面我将结合一个具体的实例，详细拆解 Prim 算法的每一步运算。

1.算法核心步骤

Prim 算法的运算可以看作是将图中的顶点分为两个集合：

集合 U（Tree Nodes）：已经被纳入最小生成树的顶点。
集合 V-U（Non-Tree Nodes）：尚未被纳入的顶点。

算法逻辑：

初始化：任选一个起始顶点放入集合 U。
寻找最短边：在所有连接集合 U 和集合 V − U 的边中（即一端在树里，一端在树外），找出权重最小的那条边。
扩展：将这条边连接的 V − U 中的那个顶点移入集合 U，并将该边加入生成树。
循环：重复步骤 2 和 3，直到 U 包含了图中的所有顶点。

2. 实例设定

为了方便你对比理解，我们继续使用刚才 Kruskal 算法用过的那个图。图包含 5 个顶点：A, B, C, D, E。

边与权重列表：

(A, B) : 权重 4
(A, C) : 权重 1
(A, D) : 权重 3
(B, C) : 权重 2
(B, D) : 权重 5
(C, D) : 权重 8
(C, E) : 权重 7
(D, E) : 权重 6

目标：求出最小生成树。 设定起点：假设我们从顶点 A 开始。

3. 详细运算步骤

初始状态

集合 U (已选点)：{A}
集合 V − U (未选点)：{B, C, D, E}
已选边：无
当前总权重：0

第1轮迭代

1.寻找最短边

我们需要考察所有从 A（U中）出发，连接到 {B, C, D, E}（V − U中）的边：

边 (A, B)，权重 4
边 (A, C)，权重 1
边 (A, D)，权重 3

2.比较与决策

最小的权重是 1，对应的边是 (A, C)。对应的树外顶点是 C。

3.更新状态

将 C 加入集合 U。
将边 (A, C) 加入生成树。
当前状态：
- 集合 U：{A, C}
- 集合 V − U：{B, D, E}
- 已选边：{(A, C)}
- 总权重：0 + 1 = 1

第2轮迭代

1.寻找最短边

现在 U = {A, C}。我们需要考察所有从一个在 {A, C} 中的点出发，连接到 {B, D, E} 中的点的边。

从 A 出发的候选边：
- (A, B)：权重 4（B 在树外，有效）
- (A, D)：权重 3（D 在树外，有效）
- (A, C)：已在树内，忽略。
从 C 出发的候选边：
- (C, B)：权重 2（B 在树外，有效）
- (C, D)：权重 8（D 在树外，有效）
- (C, E)：权重 7（E 在树外，有效） 所有候选边汇总：(A, B) : 4, (A, D) : 3, (C, B) : 2, (C, D) : 8, (C, E) : 7。

2.比较与决策

最小的权重是 2，对应的边是 (C, B)。对应的树外顶点是 B。

3.更新状态

将 B 加入集合 U。
将边 (C, B) 加入生成树。
当前状态：
- 集合 U：{A, C, B}
- 集合 V − U：{D, E}
- 已选边：{(A, C), (C, B)}
- 总权重：1 + 2 = 3

第 3 轮迭代

1.寻找最短边

现在 U = {A, C, B}，V − U = {D, E}。考察跨越这两个集合的边。

从 A 出发：(A, D) : 3（有效）。
从 C 出发：
- (C, D) : 8（有效）。
- (C, E) : 7（有效）。
从 B 出发：
- (B, D) : 5（有效）。
- (B, C): 已在树内，忽略。
- (B, A): 已在树内，忽略。

所有候选边汇总：(A, D) : 3, (C, D) : 8, (C, E) : 7, (B, D) : 5。

2.比较与决策

最小的权重是 3，对应的边是 (A, D)。对应的树外顶点是 D。

3.更新状态

将 D 加入集合 U。
将边 (A, D) 加入生成树。
当前状态：
- 集合 U：{A, C, B, D}
- 集合 V − U：{E}
- 已选边：{(A, C), (C, B), (A, D)}
- 总权重：3 + 3 = 6

第 4 轮迭代

1.寻找最短边

现在 U = {A, C, B, D}，只剩下 E 在树外。考察谁连着 E。

从 A, B, C 出发：没有直接连向 E 的边。
从 D 出发：
- (D, E) : 6（有效）。

所有候选边汇总：(D, E) : 6。

2.比较与决策

唯一的候选边权重是 6。选中 (D, E)。对应的树外顶点是 E。

3.更新状态

将 E 加入集合 U。
将边 (D, E) 加入生成树。
当前状态：
- 集合 U：{A, C, B, D, E}
- 集合 V − U：∅ (空集)
- 已选边：{(A, C), (C, B), (A, D), (D, E)}
- 总权重：6 + 6 = 12

第 5 轮迭代

由于集合 V − U 已经为空，所有顶点都已纳入生成树。算法结束。

4. 最终结果

通过 Prim 算法，我们构建出的最小生成树包含以下边：

(A, C)
(C, B)
(A, D)
(D, E)

最小生成树的总权重 = 1 + 2 + 3 + 6 = 12 (注：虽然边的添加顺序与 Kruskal 算法不同，但在同一个图中，最小生成树的总权重和结构通常是唯一的，除非有等权的边存在多种选择。)

Prim vs Kruskal 的运算区别

为了帮助记忆，我们可以对比一下：

特性	Kruskal 算法	Prim 算法
视角	边视角：全局看哪条边最短。	点视角：局部看哪个离树最近。
运算过程	1. 给所有边排序。 2. 从小到大选边。 3. 选边时判断是否形成环。	1. 任选起点。 2. 每次找“树内点”到“树外点”的最短连线。 3. 直接纳入新点（不需要判断环，因为本来就不连通）。
适用场景	适合稀疏图（边较少），因为边排序后很快就能找到结果。	适合稠密图（点少边多），或者已经给出邻接矩阵的情况。