Dijkstra算法求最短路径

1.什么是 Dijkstra 算法（标号法）？

Dijkstra 算法用于在一个带权有向图（通常权值非负）中，从指定的起点出发，求出该起点到图中所有其他顶点的最短路径。

“标号法”这个名字来源于它的操作方式：算法过程中，每个顶点都会被赋予一个标号。

2.实例设定

• T 标号（Temporary Label，临时标号）：表示从起点到该点的暂时的最短路径长度估计值。随着算法进行，T 标号会不断变小（被修正）。
• P 标号（Permanent Label，永久标号）：表示从起点到该点的真正的最短路径长度已经找到了，不再改变。一旦一个顶点获得 P 标号，它就相当于被“确定”了。

假设我们有如下所示的带权有向图，设起点为V₁，我们需要求V₁到其他所有点的最短路径：

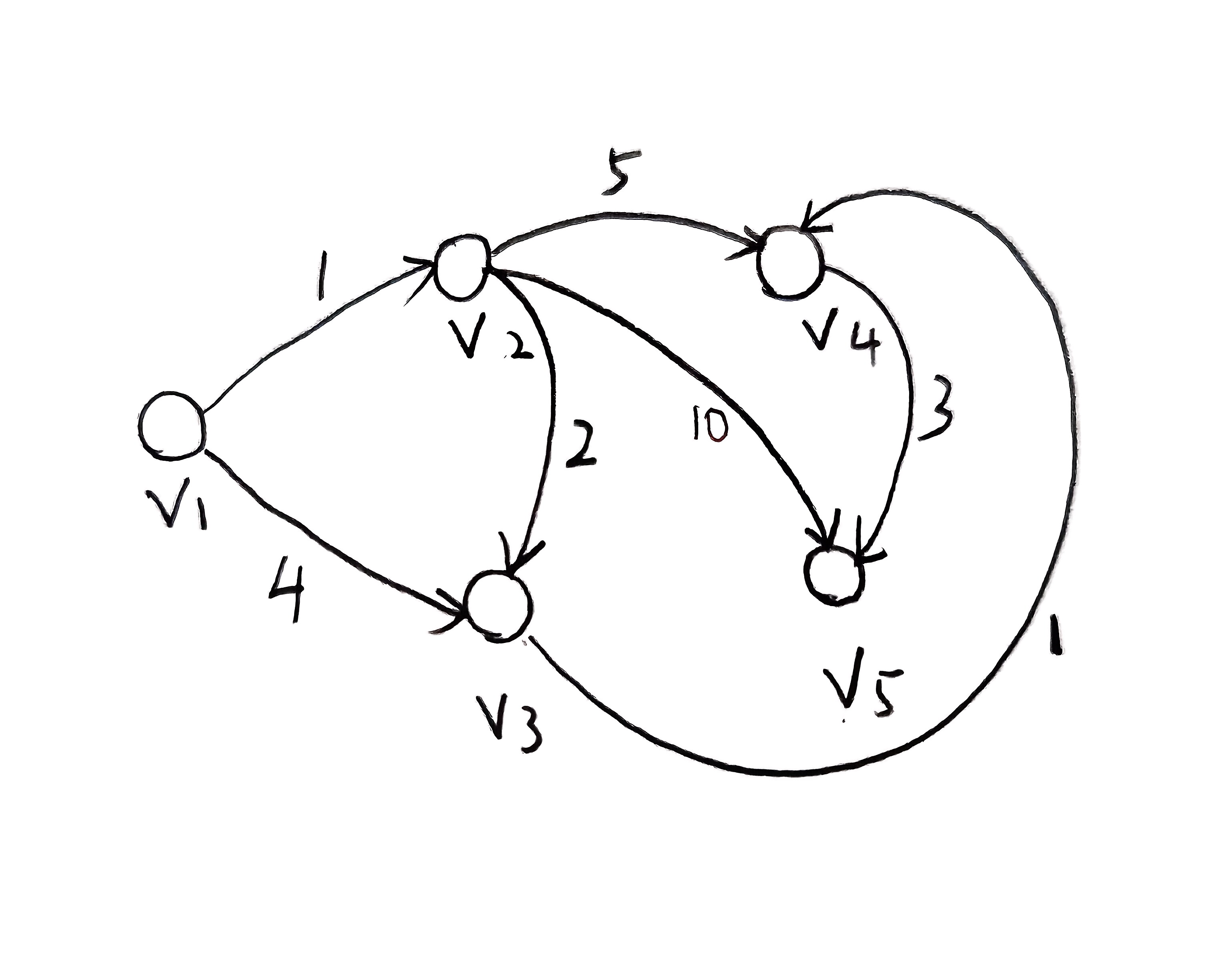
(注意：如果两点之间没有直接连线，可以理解为权重无穷大 ∞)

图的边及权重（邻接关系）：

• V₁ → V₂ (权重1)
• V₁ → V₃ (权重4)
• V₂ → V₃ (权重2)
• V₂ → V₄ (权重5)
• V₂ → V₅ (权重10)
• V₃ → V₄ (权重1)
• V₄ → V₅ (权重3)

3.算法详细步骤演示

初始状态：

• 起点V₁:设为P标号值为 0。记作P(V₁) = 0。
• 其他所有点(V₂, V₃, V₄, V₅):全部设为T标号，初始值为∞
• 前驱节点:用于记录路径，初始为空。

第1轮迭代:从V₁出发

1.修改T标号

我们要检查刚刚获得P标号的点(现在是V₁)的所有邻居。 计算方法:新T标号 = 起点P值 + 边的权重

• 邻居V₂:
  • 当前T(V₂) = ∞
  • 计算新路径:P(V₁) + Weight(V₁, V₂) = 0 + 1 = 1
  • 1 < ∞，所以更新T(V₂) = 1。
• 邻居V₃:
  • 当前T(V₃) = ∞
  • 计算新路径:P(V₁) + Weight(V₁, V₃) = 0 + 4 = 4
  • 4 < ∞，所以更新T(V₃) = 4。

2.确定P标号

在所有 T 标号中寻找最小值:

• T(V₂) = 1
• T(V₃) = 4
• T(V₄) = ∞
• T(V₅) = ∞

最小值是 1(对应的点是V₂)。 所以，将V₂的T标号改为P标号:P(V₂) = 1。 记录路径:V₁ → V₂。

当前状态:P(V₁) = 0, P(V₂) = 1。其他T(V₃) = 4, T(V₄) = ∞, T(V₅) = ∞。

第2轮迭代:从V₂出发

1.修改T标号

我们要检查新获得P标号的点(V₂)的所有邻居。 注意:V₂连接着V₃, V₄, V₅

• 邻居V₃:
  • 当前T(V₃) = 4
  • 计算新路径:P(V₂) + Weight(V₂, V₃) = 1 + 2 = 3
  • 3 < 4，我们发现这条路更短，所以更新T(V₃) = 3。
  • (这意味着路径V₁ → V₂ → V₃比V₁ → V₃更短)
• 邻居V₄:
  • 当前T(V₄) = ∞
  • 计算新路径:P(V₂) + Weight(V₂, V₄) = 1 + 5 = 6
  • 6 < ∞，所以更新T(V₄) = 6。
• 邻居V₅:
  • 当前T(V₅) = ∞
  • 计算新路径:P(V₂) + Weight(V₂, V₅) = 1 + 10 = 11
  • 11 < ∞，所以更新T(V₅) = 11。

2.确定P标号

在所有 T 标号中寻找最小值:

• T(V₃) = 3(刚刚更新的)
• T(V₄) = 6
• T(V₅) = 11

最小值是3(对应的点是V₃)。 所以，将V₃的T标号改为P标号:P(V₃) = 3。 记录路径:V₁ → V₂ → V₃。

当前状态:P(V₁) = 0, P(V₂) = 1, P(V₃) = 3。其他T(V₄) = 6, T(V₅) = 11。

第3轮迭代:从V₃出发

1.修改T标号

检查新获得P标号的点(V₃)的所有邻居。 注意:V₃连接着V₄

• 邻居V₄:
  • 当前T(V₄) = 6
  • 计算新路径:P(V₃) + Weight(V₃, V₄) = 3 + 1 = 4
  • 4 < 6，我们发现这条路更短，所以更新T(V₄) = 4。
  • (这意味着路径V₁ → V₂ → V₃ → V₄比V₁ → V₂ → V₄更短)

2.确定P标号

在所有 T 标号中寻找最小值:

• T(V₄) = 4(刚刚更新的)
• T(V₅) = 11

最小值是4(对应的点是V₄)。 所以，将V₄的T标号改为P标号:P(V₄) = 4。 记录路径:V₁ → V₂ → V₃ → V₄。

当前状态:P(V₁) = 0, P(V₂) = 1, P(V₃) = 3, P(V₄) = 4。其他T(V₅) = 11。

第4轮迭代:从V₄出发

1.修改T标号

检查新获得P标号的点(V₄)的所有邻居。 注意:V₃连接着V₅

• 邻居V₅:
  • 当前T(V₅) = 11
  • 计算新路径:P(V₄) + Weight(V₄, V₅) = 4 + 3 = 7
  • 7 < 11，我们发现这条路更短，所以更新T(V₅) = 7。
  • (这意味着路径V₁ → V₂ → V₃ → V₄ → V₅比V₁ → V₂ → V₅更短)

2.确定P标号

在所有 T 标号中寻找最小值:

• T(V₅) = 7(刚刚更新的)

最小值是7(对应的点是V₅)。 所以，将V₅的T标号改为P标号:P(V₅) = 7。 记录路径:V₁ → V₂ → V₃ → V₄ → V₅。

当前状态:所有定点都已获得P标号，算法结束。

4.最终结果汇总

通过上述每步的运算，我们得出了从起点V₁到所有其他点的最短路径长度及具体路线：

目标点	最短距离	最短路径
V1	0	V1(起点)
V2	1	V1 → V2
V3	3	V1 → V2 → V3
V4	4	V1 → V2 → V3 → V4
V5	7	V1 → V2 → V3 → V4 → V5

5.总结

如果在考试或做题中遇到此类问题，只需记住以下核心步骤： 1. 选P:在所有 T 标号中选一个最小的，改为 P 标号。 2. 改 T：以这个新 P 点为跳板，看它通向哪里。 - 公式 : 新长度 = 新P点值 + 边的权重 - 比较 : 如果新长度 < 邻居当前的T标号，则更新邻居的 T 标号。 3. 循环:重复以上两步，直到所有点都变成 P 标号。

这就是 Dijkstra 标号法的全部过程。